本文共 17861 字,大约阅读时间需要 59 分钟。
说到线程,我想大家都不陌生,因为在开发时候或多或少都会用到线程,而通常创建线程有两种方式:
1、继承Thread类
2、实现Runnable接口
虽说这两种方式都可以创建出一个线程,不过它们之间还是有一点区别的,主要区别在于在多线程访问同一资源的情况下,用Runnable接口创建的线程可以处理同一资源,而用Thread类创建的线程则各自独立处理,各自拥有自己的资源。
所以,在Java中大多数多线程程序都是通过实现Runnable来完成的,而对于Android来说也不例外,当涉及到需要开启线程去完成某件事时,我们都会这样写:
new Thread(new Runnable() { @Override public void run() { //do sth . } }).start(); 这段代码创建了一个线程并执行,它在任务结束后GC会自动回收该线程,一切看起来如此美妙,是的,它在线程并发不多的程序中确实不错,而假如这个程序有很多地方需要开启大量线程来处理任务,那么如果还是用上述的方式去创建线程处理的话,那么将导致系统的性能表现的非常糟糕,更别说在内存有限的移动设备上,主要的影响如下:
1、线程的创建和销毁都需要时间,当有大量的线程创建和销毁时,那么这些时间的消耗则比较明显,将导致性能上的缺失
2、大量的线程创建、执行和销毁是非常耗cpu和内存的,这样将直接影响系统的吞吐量,导致性能急剧下降,如果内存资源占用的比较多,还很可能造成OOM
3、大量的线程的创建和销毁很容易导致GC频繁的执行,从而发生内存抖动现象,而发生了内存抖动,对于移动端来说,最大的影响就是造成界面卡顿
而针对上述所描述的问题,解决的办法归根到底就是:重用已有的线程,从而减少线程的创建。
所以这就涉及到线程池(ExecutorService)的概念了,线程池的基本作用就是进行线程的复用,下面将具体介绍线程池的使用ExecutorService
通过上述分析,我们知道了通过new Thread().start()方式创建线程去处理任务的弊端,而为了解决这些问题,Java为我们提供了ExecutorService线程池来优化和管理线程的使用
使用线程池管理线程的优点
1、线程的创建和销毁由线程池维护,一个线程在完成任务后并不会立即销毁,而是由后续的任务复用这个线程,从而减少线程的创建和销毁,节约系统的开销
2、线程池旨在线程的复用,这就可以节约我们用以往的方式创建线程和销毁所消耗的时间,减少线程频繁调度的开销,从而节约系统资源,提高系统吞吐量
3、在执行大量异步任务时提高了性能
4、Java内置的一套ExecutorService线程池相关的api,可以更方便的控制线程的最大并发数、线程的定时任务、单线程的顺序执行等
ExecutorService简介
通常来说我们说到线程池第一时间想到的就是它:ExecutorService,它是一个接口,其实如果要从真正意义上来说,它可以叫做线程池的服务,因为它提供了众多接口api来控制线程池中的线程,而真正意义上的线程池就是:ThreadPoolExecutor,它实现了ExecutorService接口,并封装了一系列的api使得它具有线程池的特性,其中包括工作队列、核心线程数、最大线程数等。
线程池:ThreadPoolExecutor
既然线程池就是ThreadPoolExecutor,所以我们要创建一个线程池只需要new ThreadPoolExecutor(…);就可以创建一个线程池,而如果这样创建线程池的话,我们需要配置一堆东西,非常麻烦,我们可以看一下它的构造方法就知道了:
public ThreadPoolExecutor(int corePoolSize, int maximumPoolSize, long keepAliveTime, TimeUnit unit, BlockingQueueworkQueue, ThreadFactory threadFactory, RejectedExecutionHandler handler) { ...}
所以,官方也不推荐使用这种方法来创建线程池,而是推荐使用Executors的工厂方法来创建线程池,Executors类是官方提供的一个工厂类,它里面封装好了众多功能不一样的线程池,从而使得我们创建线程池非常的简便,主要提供了如下五种功能不一样的线程池:
1、newFixedThreadPool() :
作用:该方法返回一个固定线程数量的线程池,该线程池中的线程数量始终不变,即不会再创建新的线程,也不会销毁已经创建好的线程,自始自终都是那几个固定的线程在工作,所以该线程池可以控制线程的最大并发数。 栗子:假如有一个新任务提交时,线程池中如果有空闲的线程则立即使用空闲线程来处理任务,如果没有,则会把这个新任务存在一个任务队列中,一旦有线程空闲了,则按FIFO方式处理任务队列中的任务。2、newCachedThreadPool() :
作用:该方法返回一个可以根据实际情况调整线程池中线程的数量的线程池。即该线程池中的线程数量不确定,是根据实际情况动态调整的。 栗子:假如该线程池中的所有线程都正在工作,而此时有新任务提交,那么将会创建新的线程去处理该任务,而此时假如之前有一些线程完成了任务,现在又有新任务提交,那么将不会创建新线程去处理,而是复用空闲的线程去处理新任务。那么此时有人有疑问了,那这样来说该线程池的线程岂不是会越集越多?其实并不会,因为线程池中的线程都有一个“保持活动时间”的参数,通过配置它,如果线程池中的空闲线程的空闲时间超过该“保存活动时间”则立刻停止该线程,而该线程池默认的“保持活动时间”为60s。3、newSingleThreadExecutor() :
作用:该方法返回一个只有一个线程的线程池,即每次只能执行一个线程任务,多余的任务会保存到一个任务队列中,等待这一个线程空闲,当这个线程空闲了再按FIFO方式顺序执行任务队列中的任务。4、newScheduledThreadPool() :
作用:该方法返回一个可以控制线程池内线程定时或周期性执行某任务的线程池。5、newSingleThreadScheduledExecutor() :
作用:该方法返回一个可以控制线程池内线程定时或周期性执行某任务的线程池。只不过和上面的区别是该线程池大小为1,而上面的可以指定线程池的大小。
好了,写了一堆来介绍这五种线程池的作用,接下来就是获取这五种线程池,通过Executors的工厂方法来获取:
ExecutorService fixedThreadPool = Executors.newFixedThreadPool(5); ExecutorService singleThreadPool = Executors.newSingleThreadExecutor(); ExecutorService cachedThreadPool = Executors.newCachedThreadPool(); ScheduledExecutorService scheduledThreadPool = Executors.newScheduledThreadPool(5); ScheduledExecutorService singleThreadScheduledPool = Executors.newSingleThreadScheduledExecutor();
我们可以看到通过Executors的工厂方法来创建线程池极其简便,其实它的内部还是通过new ThreadPoolExecutor(…)的方式创建线程池的,我们看一下这些工厂方法的内部实现:
public static ExecutorService newFixedThreadPool(int nThreads) { return new ThreadPoolExecutor(nThreads, nThreads, 0L, TimeUnit.MILLISECONDS, new LinkedBlockingQueue ()); } public static ExecutorService newSingleThreadExecutor() { return new FinalizableDelegatedExecutorService (new ThreadPoolExecutor(1, 1, 0L, TimeUnit.MILLISECONDS, new LinkedBlockingQueue ())); } public static ExecutorService newCachedThreadPool() { return new ThreadPoolExecutor(0, Integer.MAX_VALUE, 60L, TimeUnit.SECONDS, new SynchronousQueue ()); } 我们可以清楚的看到这些方法的内部实现都是通过创建一个ThreadPoolExecutor对象来创建的,正所谓万变不离其宗,所以我们要了解线程池还是得了解ThreadPoolExecutor这个线程池类,其中由于和定时任务相关的线程池比较特殊(newScheduledThreadPool()、newSingleThreadScheduledExecutor()),它们创建的线程池内部实现是由ScheduledThreadPoolExecutor这个类实现的,而ScheduledThreadPoolExecutor是继承于ThreadPoolExecutor扩展而成的,所以本质还是一样的,只不过多封装了一些定时任务相关的api,所以我们主要就是要了解ThreadPoolExecutor,从构造方法开始:
public ThreadPoolExecutor(int corePoolSize, int maximumPoolSize, long keepAliveTime, TimeUnit unit, BlockingQueueworkQueue, ThreadFactory threadFactory, RejectedExecutionHandler handler) {//...}
我们可以看到它构造方法的参数比较多,有七个,下面一一来说明这些参数的作用:
corePoolSize:线程池中的核心线程数量
maximumPoolSize:线程池中的最大线程数量 keepAliveTime:这个就是上面说到的“保持活动时间“,上面只是大概说明了一下它的作用,不过它起作用必须在一个前提下,就是当线程池中的线程数量超过了corePoolSize时,它表示多余的空闲线程的存活时间,即:多余的空闲线程在超过keepAliveTime时间内没有任务的话则被销毁。而这个主要应用在缓存线程池中 unit:它是一个枚举类型,表示keepAliveTime的单位,常用的如:TimeUnit.SECONDS(秒)、TimeUnit.MILLISECONDS(毫秒) workQueue:任务队列,主要用来存储已经提交但未被执行的任务,不同的线程池采用的排队策略不一样,稍后再讲 threadFactory:线程工厂,用来创建线程池中的线程,通常用默认的即可 handler:通常叫做拒绝策略,1、在线程池已经关闭的情况下 2、任务太多导致最大线程数和任务队列已经饱和,无法再接收新的任务 。在上面两种情况下,只要满足其中一种时,在使用execute()来提交新的任务时将会拒绝,而默认的拒绝策略是抛一个RejectedExecutionException异常
上面的参数理解起来都比较简单,不过workQueue这个任务队列却要再次说明一下,它是一个BlockingQueue<Runnable>对象,而泛型则限定它是用来存放Runnable对象的,刚刚上面讲了,不同的线程池它的任务队列实现肯定是不一样的,所以,保证不同线程池有着不同的功能的核心就是这个workQueue的实现了,细心的会发现在刚刚的用来创建线程池的工厂方法中,针对不同的线程池传入的workQueue也不一样,下面我总结一下这五种线程池分别用的是什么BlockingQueue:
1、newFixedThreadPool()—>LinkedBlockingQueue
2、newSingleThreadExecutor()—>LinkedBlockingQueue 3、newCachedThreadPool()—>SynchronousQueue 4、newScheduledThreadPool()—>DelayedWorkQueue 5、newSingleThreadScheduledExecutor()—>DelayedWorkQueue
这些队列分别表示:
LinkedBlockingQueue:无界的队列
SynchronousQueue:直接提交的队列 DelayedWorkQueue:等待队列
当然实现了BlockingQueue接口的队列还有:ArrayBlockingQueue(有界的队列)、PriorityBlockingQueue(优先级队列)。这些队列的详细作用就不多介绍了。
线程池ThreadPoolExecutor的使用
使用线程池,其中涉及到一个极其重要的方法,即:
execute(Runnable command)
该方法意为执行给定的任务,该任务处理可能在新的线程、已入池的线程或者正调用的线程,这由ThreadPoolExecutor的实现决定。
newFixedThreadPool 创建一个固定线程数量的线程池,示例为:ExecutorService fixedThreadPool = Executors.newFixedThreadPool(3); for (int i = 1; i <= 10; i++) { final int index = i; fixedThreadPool.execute(new Runnable() { @Override public void run() { String threadName = Thread.currentThread().getName(); Log.v("zxy", "线程:"+threadName+",正在执行第" + index + "个任务"); try { Thread.sleep(2000); } catch (InterruptedException e) { e.printStackTrace(); } } }); } 上述代码,我们创建了一个线程数为3的固定线程数量的线程池,同理该线程池支持的线程最大并发数也是3,而我模拟了10个任务让它处理,执行的情况则是首先执行前三个任务,后面7个则依次进入任务队列进行等待,执行完前三个任务后,再通过FIFO的方式从任务队列中取任务执行,直到最后任务都执行完毕。
为了体现出线程的复用,我特地在Log中加上了当前线程的名称,效果为: newSingleThreadExecutor 创建一个只有一个线程的线程池,每次只能执行一个线程任务,多余的任务会保存到一个任务队列中,等待线程处理完再依次处理任务队列中的任务,示例为:
newSingleThreadExecutor 创建一个只有一个线程的线程池,每次只能执行一个线程任务,多余的任务会保存到一个任务队列中,等待线程处理完再依次处理任务队列中的任务,示例为: ExecutorService singleThreadPool = Executors.newSingleThreadExecutor(); for (int i = 1; i <= 10; i++) { final int index = i; singleThreadPool.execute(new Runnable() { @Override public void run() { String threadName = Thread.currentThread().getName(); Log.v("zxy", "线程:"+threadName+",正在执行第" + index + "个任务"); try { Thread.sleep(1000); } catch (InterruptedException e) { e.printStackTrace(); } } }); } 代码还是差不多,只不过改了线程池的实现方式,效果我想大家都知道,即依次一个一个的处理任务,而且都是复用一个线程,效果为:

其实我们通过newSingleThreadExecutor()和newFixedThreadPool()的方法发现,创建一个singleThreadExecutorPool实际上就是创建一个核心线程数和最大线程数都为1的fixedThreadPool。
newCachedThreadPool 创建一个可以根据实际情况调整线程池中线程的数量的线程池,示例为:ExecutorService cachedThreadPool = Executors.newCachedThreadPool(); for (int i = 1; i <= 10; i++) { final int index = i; try { Thread.sleep(1000); } catch (InterruptedException e) { e.printStackTrace(); } cachedThreadPool.execute(new Runnable() { @Override public void run() { String threadName = Thread.currentThread().getName(); Log.v("zxy", "线程:" + threadName + ",正在执行第" + index + "个任务"); try { long time = index * 500; Thread.sleep(time); } catch (InterruptedException e) { e.printStackTrace(); } } }); } 为了体现该线程池可以自动根据实现情况进行线程的重用,而不是一味的创建新的线程去处理任务,我设置了每隔1s去提交一个新任务,这个新任务执行的时间也是动态变化的,所以,效果为:
 newScheduledThreadPool 创建一个可以定时或者周期性执行任务的线程池,示例为:
newScheduledThreadPool 创建一个可以定时或者周期性执行任务的线程池,示例为: ScheduledExecutorService scheduledThreadPool = Executors.newScheduledThreadPool(3); //延迟2秒后执行该任务 scheduledThreadPool.schedule(new Runnable() { @Override public void run() { } }, 2, TimeUnit.SECONDS); //延迟1秒后,每隔2秒执行一次该任务 scheduledThreadPool.scheduleAtFixedRate(new Runnable() { @Override public void run() { } }, 1, 2, TimeUnit.SECONDS); newSingleThreadScheduledExecutor
创建一个可以定时或者周期性执行任务的线程池,该线程池的线程数为1,示例为:ScheduledExecutorService singleThreadScheduledPool = Executors.newSingleThreadScheduledExecutor(); //延迟1秒后,每隔2秒执行一次该任务 singleThreadScheduledPool.scheduleAtFixedRate(new Runnable() { @Override public void run() { String threadName = Thread.currentThread().getName(); Log.v("zxy", "线程:" + threadName + ",正在执行"); } },1,2,TimeUnit.SECONDS); 实际上这个和上面的没什么太大区别,只不过是线程池内线程数量的不同,效果为:
 每隔2秒就会执行一次该任务
每隔2秒就会执行一次该任务 自定义线程池ThreadPoolExecutor
Java内置只为我们提供了五种常用的线程池,一般来说这足够用了,不过有时候我们也可以根据需求来自定义我们自己的线程池,而要自定义不同功能的线程池,上面我们也说了线程池功能的不同归根到底还是内部的BlockingQueue实现不同,所以,我们要实现我们自己相要的线程池,就必须从BlockingQueue的实现上做手脚,而上面也说了BlockingQueue的实现类有多个,那么这次我们就选用PriorityBlockingQueue来实现一个功能是按任务的优先级来处理的线程池。
1、首先我们创建一个基于PriorityBlockingQueue实现的线程池,为了测试方便,我这里把核心线程数量设置为3,如下:
ExecutorService priorityThreadPool = new ThreadPoolExecutor(3,3,0L,TimeUnit.SECONDS,new PriorityBlockingQueue());
- 1
2、然后创建一个实现Runnable接口的类,并向外提供一个抽象方法供我们实现自定义功能,并实现Comparable接口,实现这个接口主要就是进行优先级的比较,代码如下:
public abstract class PriorityRunnable implements Runnable, Comparable{ private int priority; public PriorityRunnable(int priority) { if (priority < 0) throw new IllegalArgumentException(); this.priority = priority; } @Override public int compareTo(PriorityRunnable another) { int my = this.getPriority(); int other = another.getPriority(); return my < other ? 1 : my > other ? -1 : 0; } @Override public void run() { doSth(); } public abstract void doSth(); public int getPriority() { return priority; }}
3、使用我们自己的PriorityRunnable提交任务,整体代码如下:
ExecutorService priorityThreadPool = new ThreadPoolExecutor(3, 3, 0L, TimeUnit.SECONDS, new PriorityBlockingQueue()); for (int i = 1; i <= 10; i++) { final int priority = i; priorityThreadPool.execute(new PriorityRunnable(priority) { @Override public void doSth() { String threadName = Thread.currentThread().getName(); Log.v("zxy", "线程:" + threadName + ",正在执行优先级为:" + priority + "的任务"); try { Thread.sleep(2000); } catch (InterruptedException e) { e.printStackTrace(); } } }); }
测试效果
我们看下刚刚自定义的线程池是否达到了我们想要的功能,即根据任务的优先级进行优先处理任务,效果如下:

可以从执行结果中看出,由于核心线程数设置为3,刚开始时,系统有3个空闲线程,所以无须使用任务队列,而是直接运行前三个任务,而后面再提交任务时由于当前没有空闲线程所以加入任务队列中进行等待,此时,由于我们的任务队列实现是由PriorityBlockingQueue实现的,所以进行等待的任务会经过优先级判断,优先级高的放在队列前面先处理。从效果图中也可以看到后面的任务是先执行优先级高的任务,然后依次递减。
优先级线程池的优点
从上面我们可以得知,创建一个优先级线程池非常有用,它可以在线程池中线程数量不足或系统资源紧张时,优先处理我们想要先处理的任务,而优先级低的则放到后面再处理,这极大改善了系统默认线程池以FIFO方式处理任务的不灵活
扩展线程池ThreadPoolExecutor
除了内置的功能外,ThreadPoolExecutor也向外提供了三个接口供我们自己扩展满足我们需求的线程池,这三个接口分别是:
beforeExecute() - 任务执行前执行的方法
afterExecute() -任务执行结束后执行的方法 terminated() -线程池关闭后执行的方法
这三个方法在ThreadPoolExecutor内部都没有实现
前面两个方法我们可以在ThreadPoolExecutor内部的runWorker()方法中找到,而runWorker()是ThreadPoolExecutor的内部类Worker实现的方法,Worker它实现了Runnable接口,也正是线程池内处理任务的工作线程,而Worker.runWorker()方法则是处理我们所提交的任务的方法,它会同时被多个线程访问,所以我们看runWorker()方法的实现,由于涉及到多个线程的异步调用,必然是需要使用锁来处理,而这里使用的是Lock来实现的,我们来看看runWorker()方法内主要实现:
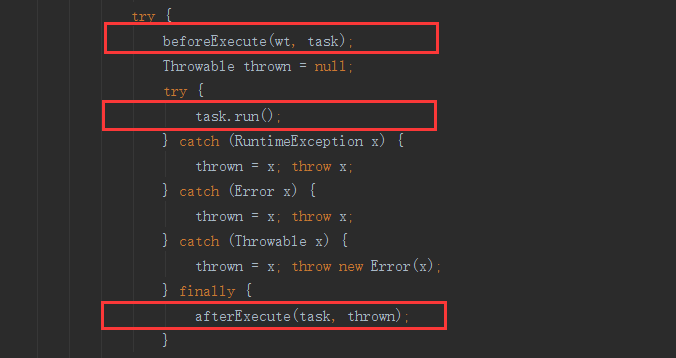
可以看到在task.run()之前和之后分别调用了beforeExecute和afterExecute方法,并传入了我们的任务Runnable对象
而terminated()则是在关闭线程池的方法中调用,而关闭线程池有两个方法,我贴其中一个:
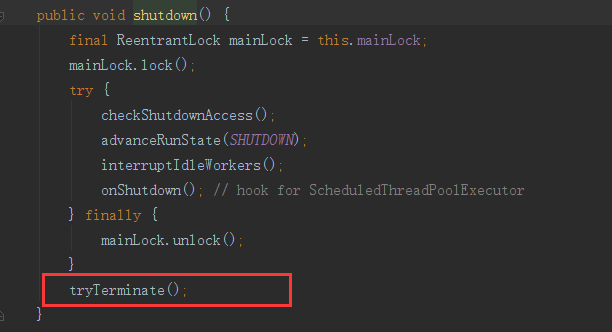
所以,我们要扩展线程池,只需要重写这三个方法,并实现我们自己的功能即可,这三个方法分别都会在任务执行前调用、任务执行完成后调用、线程池关闭后调用。
这里我验证一下,继承自ThreadPoolExecutor 并实现那三个方法:public class MyThreadPoolExecutor extends ThreadPoolExecutor { public MyThreadPoolExecutor(int corePoolSize, int maximumPoolSize, long keepAliveTime, TimeUnit unit, BlockingQueue workQueue) { super(corePoolSize, maximumPoolSize, keepAliveTime, unit, workQueue); } @Override protected void beforeExecute(Thread t, Runnable r) { super.beforeExecute(t, r); String threadName = t.getName(); Log.v("zxy", "线程:" + threadName + "准备执行任务!"); } @Override protected void afterExecute(Runnable r, Throwable t) { super.afterExecute(r, t); String threadName = Thread.currentThread().getName(); Log.v("zxy", "线程:" + threadName + "任务执行结束!"); } @Override protected void terminated() { super.terminated(); Log.v("zxy", "线程池结束!"); }} 而运行后的结果则是,这正符合刚刚说的:
11-17 05:47:51.184 1602-1619/? V/zxy: 线程:pool-6-thread-1准备执行任务!11-17 05:47:51.184 1602-1619/? V/zxy: 线程:pool-6-thread-1正在执行任务!11-17 05:47:53.184 1602-1619/? V/zxy: 线程:pool-6-thread-1任务执行结束!11-17 05:47:58.896 1602-1619/? V/zxy: 线程池结束!
所以,在上面我们的优先级线程池的代码上,我们再扩展一个具有暂停功能的优先级线程池,代码如下:
具有暂时功能的线程池:public class PausableThreadPoolExecutor extends ThreadPoolExecutor { private boolean isPaused; private ReentrantLock pauseLock = new ReentrantLock(); private Condition unpaused = pauseLock.newCondition(); public PausableThreadPoolExecutor(int corePoolSize, int maximumPoolSize, long keepAliveTime, TimeUnit unit, BlockingQueue workQueue) { super(corePoolSize, maximumPoolSize, keepAliveTime, unit, workQueue); } @Override protected void beforeExecute(Thread t, Runnable r) { super.beforeExecute(t, r); pauseLock.lock(); try { while (isPaused) unpaused.await(); } catch (InterruptedException ie) { t.interrupt(); } finally { pauseLock.unlock(); } } public void pause() { pauseLock.lock(); try { isPaused = true; } finally { pauseLock.unlock(); } } public void resume() { pauseLock.lock(); try { isPaused = false; unpaused.signalAll(); } finally { pauseLock.unlock(); } }} 然后结合上面的优先级线程池的实现,创建具有暂停功能的优先级线程池:
PausableThreadPoolExecutor pausableThreadPoolExecutor = new PausableThreadPoolExecutor(1, 1, 0L, TimeUnit.SECONDS, new PriorityBlockingQueue()); for (int i = 1; i <= 100; i++) { final int priority = i; pausableThreadPoolExecutor.execute(new PriorityRunnable(priority) { @Override public void doSth() { runOnUiThread(new Runnable() { @Override public void run() { textView.setText(priority + ""); } }); try { Thread.sleep(1000); } catch (InterruptedException e) { e.printStackTrace(); } } }); }
这里我为了演示效果,把这个线程池设为只有一个线程,然后直接在TextView中显示当前执行的任务的优先级,然后设置个开关,控制线程池的暂停与开始:
if (isPause) { pausableThreadPoolExecutor.resume(); isPause = false; } else { pausableThreadPoolExecutor.pause(); isPause = true; } 效果为:

从效果上来看,该线程池和优先级线程一样,而且还多了一个暂停与开始的功能
优化线程池ThreadPoolExecutor
虽说线程池极大改善了系统的性能,不过创建线程池也是需要资源的,所以线程池内线程数量的大小也会影响系统的性能,大了反而浪费资源,小了反而影响系统的吞吐量,所以我们创建线程池需要把握一个度才能合理的发挥它的优点,通常来说我们要考虑的因素有CPU的数量、内存的大小、并发请求的数量等因素,按需调整。
通常核心线程数可以设为CPU数量+1,而最大线程数可以设为CPU的数量*2+1。
获取CPU数量的方法为:
Runtime.getRuntime().availableProcessors();
- 1
shutdown()和shutdownNow()的区别
关于线程池的停止,ExecutorService为我们提供了两个方法:shutdown和shutdownNow,这两个方法各有不同,可以根据实际需求方便的运用,如下:
1、shutdown()方法在终止前允许执行以前提交的任务。
2、shutdownNow()方法则是阻止正在任务队列中等待任务的启动并试图停止当前正在执行的任务。
关于AsyncTask的实现
大家都知道AsyncTask内部实现其实就是Thread+Handler。其中Handler是为了处理线程之间的通信,而这个Thread到底是指什么呢?通过AsyncTask源码可以得知,其实这个Thread是线程池,AsyncTask内部实现了两个线程池,分别是:串行线程池和固定线程数量的线程池。而这个固定线程数量则是通过CPU的数量决定的。
在默认情况下,我们大都通过AsyncTask::execute()来执行任务的,
,而execute()内部则是调用executeOnExecutor(sDefaultExecutor, params)方法执行的,第一个参数就是指定处理该任务的线程池,而默认情况下AsyncTask是传入串行线程池(在这里不讲版本的变化),也就是任务只能单个的按顺序执行,而我们要是想让AsyncTask并行的处理任务,大家都知道调用AsyncTask::executeOnExecutor(sDefaultExecutor, params)方法传入这个参数即可:AsyncTask.THREAD_POOL_EXECUTOR。 而这个参数的意义在于为任务指定了一个固定线程数量的线程池去处理,从而达到了并行处理的功能,我们可以在源码中看到AsyncTask.THREAD_POOL_EXECUTOR这个参数就是一个固定线程数量的线程池:public static final Executor THREAD_POOL_EXECUTOR = new ThreadPoolExecutor(CORE_POOL_SIZE, MAXIMUM_POOL_SIZE, KEEP_ALIVE, TimeUnit.SECONDS, sPoolWorkQueue, sThreadFactory);